If you have come from Dungeons & Dragons, Pathfinder, or the like, you may know of the “Action Economy.” In short, it’s a way of measuring how much player characters (PCs) can act compared to enemies in combat. Although Daggerheart focuses more on cinematic combat, the tactical component is still there, so there still is a Daggerheart Action Economy.
This post will be a bit of game design, a bit of math, some nice graphs, and finally advice to players and GMs.
So let’s dive into it.
The design of Daggerheart combat actions
In addition to D&D, Daggerheart takes inspiration from systems like Powered by the Apocalypse (PbtA). In PbtA, the GM makes a move when a player fails a roll. For example in Dungeon World, if a player rolls a 6 or lower on “Discern Realities”, the GM can respond with “Use up their Resources.”
Like the example above, this applies in and out of combat. And in combat, the GM doesn’t have to “Deal damage,” though they usually will. This back-and-forth is intended to create a “fail forward” sort of mentality.
In D&D, if a player character misses an attack, then typically nothing happens; it just moves to someone else’s turn. The strategy comes in with maximizing the use of the standard action, bonus action, free action, and movement.
In PbtA, the GM only calls for rolls if there are interesting consequences. On either success or failure, it should drive the narrative forward. Daggerheart borrows from this structure where rolling a failure or with Fear gives the spotlight back to the GM.
Compared to D&D, the most obvious difference in the Daggerheart Action Economy is that the number of players and monsters doesn’t matter. In D&D, each round of combat generally gives each participant one turn, so those twenty goblins will get five times as many actions as the four players.

In Daggerheart, all that matters is what the players rolls. Unless those goblins group up as minions, they will act just as much with twenty as with one hundred. And on each turn, you can only do as much as one action roll.
That being said, there still is some math to how much players act compared to GMs. Players keep the spotlight if they roll a success with Hope, so how much they act depends on how well they roll. How well they roll depends on probability, so here comes the math.
Oh, and one more note: I’ll be using the words “moves”, “actions”, and “spotlights” interchangeably throughout this post. They mean roughly the same thing but vary in nomenclature depending on the system.
The math of Daggerheart combat actions
(Note: If you’re interested in how I calculated all of this, see the Appendix at the bottom of this page)
Here are all of the ways that attack rolls can turn out in Daggerheart.
- Critical success. Woohoo! GM cries, good things happen for the players, blah blah blah. Players get another spotlight
- Success with Hope. PC hits. Players get another spotlight
- Success with Fear. PC hits. GM gets a spotlight and a Fear
- Failure with Hope. PC misses. GM gets a spotlight but no Fear
- Failure with Fear. PC misses. GM gets a spotlight and a Fear
So to figure out how many actions players get versus GMs, it actually matters what the difficulty of the roll is. If it’s a low difficulty (e.g. 5) or the PC has high modifiers (e.g. +6), then they are more likely to succeed and get the spotlight back. And if it’s hard, the adversaries are more likely to get a turn.
With a bit of math, we get one nice graph about the Daggerheart Action Economy.
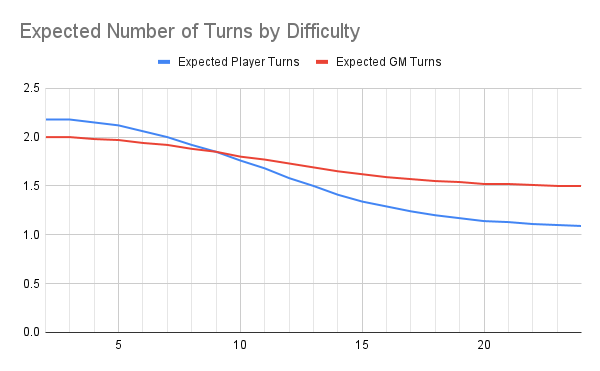
To explain, take a look at the points above the X axis at 10. This corresponds to a modified difficulty of 10, such as +0 versus difficulty 10, +1 versus difficulty 11, etc. At that point, GMs will expect to get about 1.8 actions for every 1.76 player actions.
The crossover point is at the modified difficulty of 9. If the modified difficulty is lower, then players get more turns. If the modified difficulty is higher, than the GM gets more turns.
For context, level 1 PCs will typically have a +2 attack modifier, and the tier 1 improvised adversary has a difficulty of 11. That perfectly corresponds to a modified difficulty of 9.
Now a difference of 1.8 versus 1.76 can be hard to conceptualize. Another way to look at this the percentage difference in actions taken.
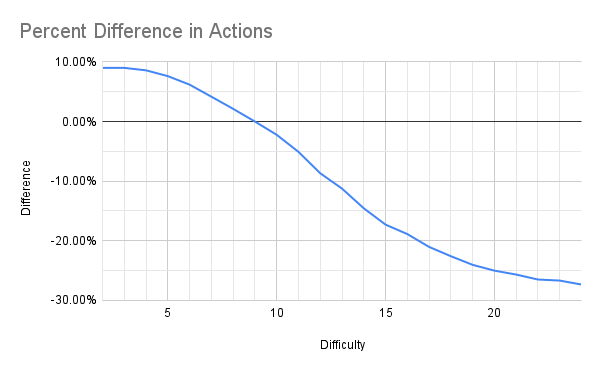
In this graph, players take 9% more actions than the GM at modified difficulty 2. This drops to 27% fewer actions at modified difficulty 24.
After you’re done staring at the graphs, let’s talk about how this information actually impacts your game.
My player advice on Daggerheart combat actions
From the player side, this likely has little impact on what you should do. Generally, you should do your best to make the most of your actions, and nothing in the math changes that.
Perhaps a small mindset change from other Action Economies is that in the Daggerheart Action Economy, picking actions with low likelihood of success actually works against you. In other tactical TTRPGs, if you make a goofy attack without proficiency, then it wastes your action, but at least it doesn’t make your enemies more effective. However, in Daggerheart, if you make a goofy attack with a low modifier, it increases the chance that the adversaries will get the spotlight.
When fighting a group of mixed adversaries, you should (all else being equal) attack the easy-to-hit targets first. If you do, then you’re more likely to keep the spotlight. However, the actual optimal strategy is significantly more complicated. All else is not equal in adversary design, so factor the spotlight in alongside, relative toughness, damage output, and more for the different adversaries.
My GM advice on Daggerheart combat actions
The biggest assumption that I made above is that GMs will turn all Fear into additional adversary spotlights, and that is definitely not true. The flexibility of Fear means that you can use it exactly as much as you need to ratchet up the tension.
When I first saw the results, I was shocked by how skewed the results were towards GM actions. However, I since realized that this is the just a ceiling on how much GMs can do: you can’t do any more, but you can always do less.
On the flip side, consider the other extreme, If the GM never spends Fear tokens, then the GM is effectively just taking 1 spotlight, which put the expected GM actions well below the players at any difficulty. That is the floor.
If you feel like you really need to use all of your Fear, remember there are all sorts of ways to spend it that aren’t spotlighting adversaries to attack. In more tactical TTRPGs, if the enemies aren’t swinging, it’s more obvious that the GM is holding back. PbtA has “soft moves” where the GM is setting up for future consequences. You can calibrate similarly in Daggerheart.
Personally as a GM, I have always disliked feeling like I’m playing more than anyone else at the table. Rather than having an audience of players, I want everyone to feel like they’re contributing roughly equally both to the drama as well as being able to roll dice.
When I ran D&D, I tried to avoid mob fights. It seemed ridiculous for me to be rolling and rolling for a dozen goblins while my players checked their phones. Instead, I preferred running boss or solo fights, though I still had to use legendary actions just for balance in the Action Economy
With the Daggerheart Action Economy, I likely will be calibrating my Fear spending to spotlight just a little less frequently than my players. I still haven’t played enough to get a feel for the balance. However, my intuition is that I’ll run a better game if I’m more creative with spending Fear rather than just hitting back.
Final thoughts on the Daggerheart Action Economy
Having run the numbers and written this post, the notion of the Action Economy works better as an abstract principle than through quantitative analysis. It reminds me of “card advantage” from Magic: the Gathering. Card advantage is a very useful heuristic and teaching tool but only a small portion of the complexity of the game.
Compared to other more tactical TTRPGs, Daggerheart also has an added dimension of being narratively-driven with PbtA-like inspiration. Combat shouldn’t (and probably can’t) be reduced down to exact probabilities of outcomes through perfectly balanced encounters because perfectly balanced encounters don’t necessarily lead to the best story and drama. Those considerations are more things for the GM and players to work together towards.
Overall, it’s actually quite reassuring that the rules fit with how you intuitively should want to play. At least with regard to managing the spotlight, you shouldn’t have too much tension between doing what’s fun and what’s optimal.
So keep the math in mind, but remember, it’s only one part of the foundation of this game.
Appendix: Showing my work
At first blush, the math for calculating the expected number of turns seems tricky. There are five different cases, and depending on which one you fall into, you get a different result impacting two separate numbers (player turns and GM turns).
In fact, I gave up after a page of scribbles and decided to do a Monte Carlo simulation. That’s where a computer simulates rolling dice thousands and thousands of times, and then we just check to see how often we got different results. You can check my code here.
However, shortly before writing this post, I realized that the player turns and GM turns are entirely separate results and can be calculated as such. The important thing is that the spotlight going to the GM is effectively the end of the round. After the GM moves, then it goes back to the player, and that’s an independent situation.
To calculate how many moves a GM makes, we only need to determine how frequently GMs get one move (fail with hope) versus two moves (success or failure with fear) when they get the spotlight. That’s
E(GM) = (2 * (P(Success with Fear) + P(Fail with Fear)) + 1 * P(Fail with Hope)) / (P(Success with Fear) + P(Fail with Fear) + P(Fail with Hope))
All of the probabilities above can be easily determined by just counting all 144 2d12 outcomes against the difficulty. I have a separate blog post covering The Math of Daggerheart’s 2d12 Duality Dice Roll.
To calculate how many moves a player gets, the player just gets one more turn every time they roll either a Critical Success or a Success with Hope. This could in theory happen infinitely, but each additional turn becomes increasingly less likely.
Fortunately, the expected value of this can be calculated as the convergence of an infinite geometric series
E(PC) = 1 / (1 – (P(Critical Success) + P(Success with Hope)))
Again, the probabilities can be determined by counting.
Of course, I could be wrong twice. I could have written a bad simulation, and I could have bad math. However, I’m feeling relatively confident right now because the results of both were very, very close. You can see the full chart of data here.
But if I’m still wrong, please let me know!
Leave a Reply